Исследовательский проект по физике: бросок монетки

Стандартный пример, который приводится в начале изучения теории вероятностей, – это бросок двухсторонней монетки. Утверждается, что события «монета упала решкой вверх» и «монета упала орлом вверх» равновероятны из-за симметрии. Мне стало интересно, как получить такой результат, используя более строгие физические рассуждения. К тому же, исследуя динамику броска, можно ответить и на другие вопросы:
- Какова вероятность, что монета встанет на ребро, и зависит ли это от ее толщины?
- Какой должна быть монета, чтобы события «падение на бок», «падение решкой вверх» и «падение орлом вверх» были равновероятны?
- Как фокусникам удаётся бросать монетку так, что всегда выпадает нужная им сторона?
Для ответов на поставленные вопросы я разобрал статью Probability, geometry, and dynamics in the toss of a thick coin.
Физическая модель
Любое исследование начинается с построения физической модели и этот случай – не исключение. Будем считать, что монета имеет форму цилиндра и состоит из однородного материала (важно, что толщиной монеты мы не пренебрегаем). В начальный момент времени монета находится на высоте h над неупругой поверхностью, имеет вертикально направленную скорость и произвольно вращается. Далее делаем существенное упрощение: монета падает на поверхность без отскока.
Для того чтобы определить, на какую сторону упадет монетка, я решил посмотреть, как от времени зависит вектор нормали, проведенной к плоскости верхней грани. Например, если в момент падения вектор направлен вверх, мы получаем событие «монета упала верхней гранью вверх». Далее я связал изменение направления нормали с вектором угловой скорости, а угловую скорость выразил через момент импульса. Из-за того, что монета имеет цилиндрическую форму, тензор инерции устроен так, что нормаль просто вращается вокруг вектора момента импульса с постоянной угловой скоростью.
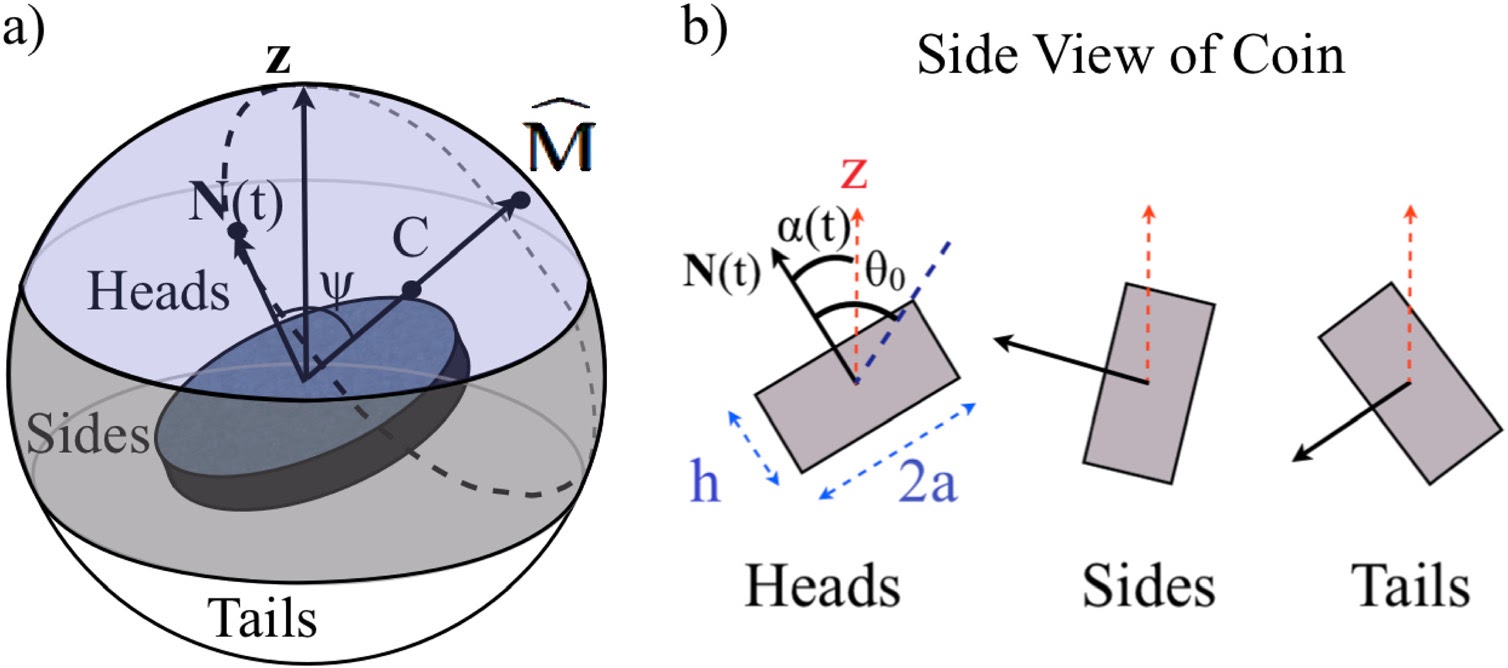
Пунктиром на рисунке (a) показано, как вектор нормали N вращается вокруг вектора момента импульса M. Заметим, что окружность, которую описывает вектор N, проходит через «северный полюс» сферы, потому что в начальный момент времени вектор N направлен вверх.
На рисунке (б) показано, как направление вектора N влияет на исход броска.
Исход броска зависит от угла α(t) – угол между N и осью z. Условие на каждое из трех событий можно записать через простые неравенства. Сам α(t) я получил, используя сферическую теорему косинусов и факт о вращении вектора N. Далее через начальную скорость и этот угол можно выразить момент времени, когда монетка столкнется с поверхностью. Из-за того, что при броске мы придаем случайные вертикальные и угловые скорости, момент времени падения t₁ тоже оказывается случайно распределен. Я предположил, что малые случайные изменения начальных параметров влекут большие изменения угла α(t₁), поэтому можно считать, что момент падения t₁ равномерно распределен в рамках периода вращения вектораN.
В итоге я получил следующий результат: вероятности трёх исходов зависят от двух начальных параметров – относительной ширины монеты (отношение толщины к диаметру) и угла между начальным моментом импульса и осью z. Для наглядности можно обратиться к графикам из статьи:
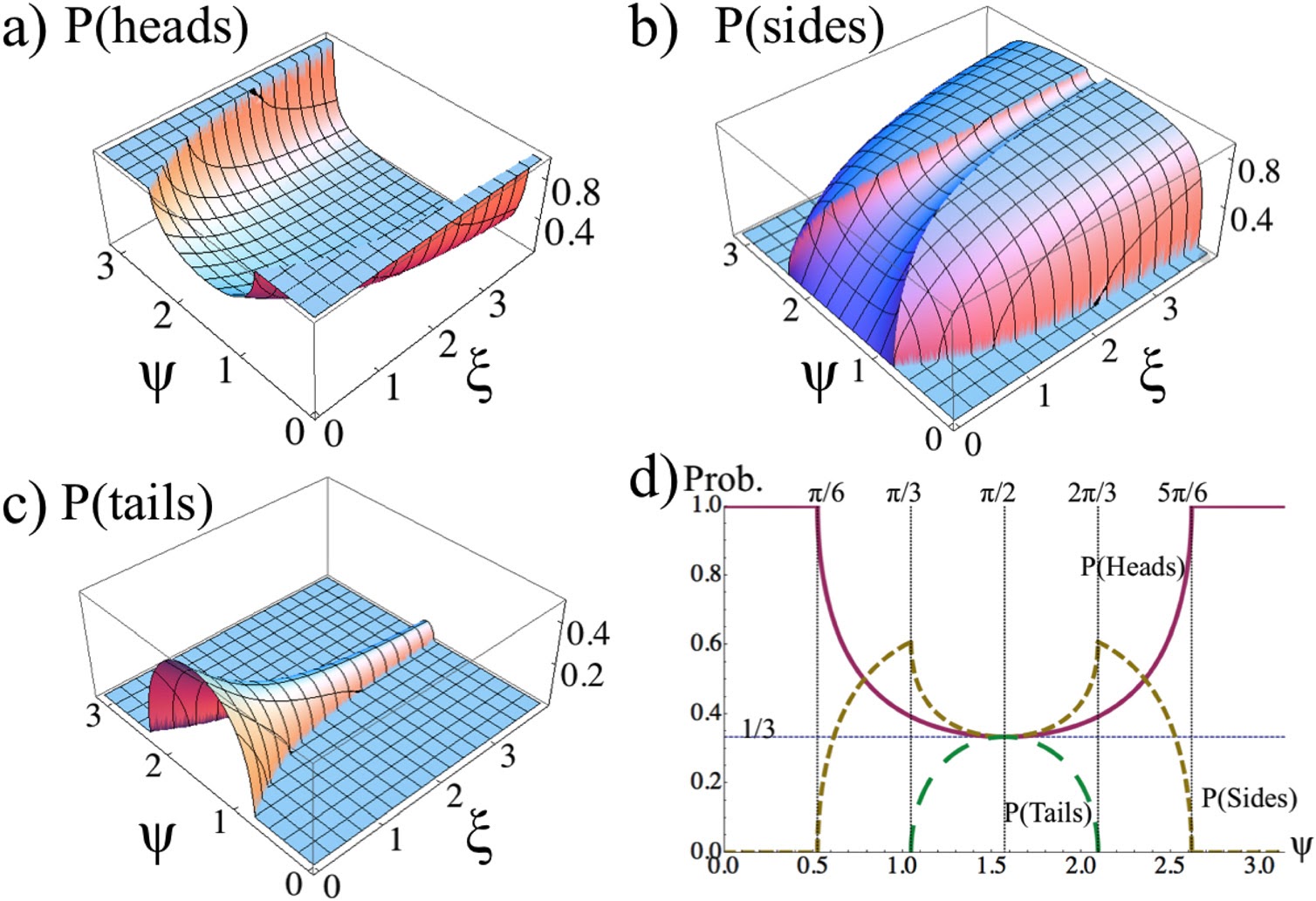
На рисунках (a), (b) и (c) показаны вероятности трёх событий в зависимости от параметров: ζ – относительная ширина, ψ – угол между M и осью z. На рисунке (d) показана зависимость всех трёх вероятностей от угла ψ при такой относительной ширине, что все три события равновероятны («справедливая» трёхсторонняя монетка).
Решение
Уже с полученными явными математическими формулами для P(ζ, ψ) я принялся отвечать на поставленные вопросы. Взглянув на формулы, я пришел к достаточно неожиданным выводам: если ψ = π/2 (момент импульса лежит в плоскости монетки), то выпадение верхней и нижней стороны монетки равновероятно, но при ψ ≠ π/2 выпадение верхней стороны становится более вероятным. Это значит, что если во время броска немного подкрутить монету вокруг вертикальной оси, то на монете чаще будет выпадать та же сторона, что и была направлена вверх в начале броска. При этом вращение при таком броске визуально ничем не отличается от обычного броска. Именно в этом и заключается секрет фокуса.
Далее, исследуя зависимости вероятностей от толщины, я принял угол ψ равным π/2 и построил график этой зависимости:
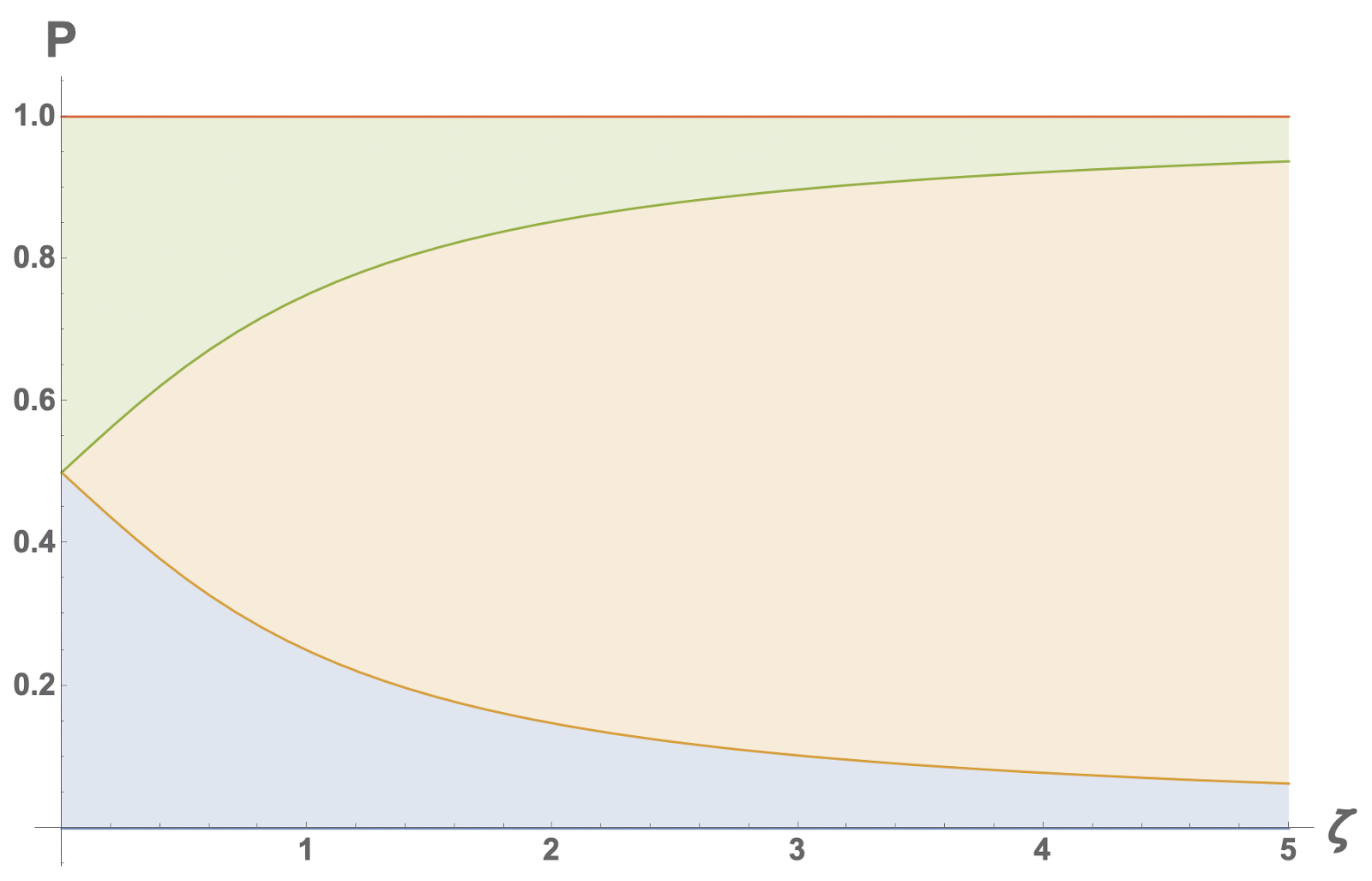
На графике синим цветом заливки обозначена вероятность события «падение решкой вверх», оранжевым – «падение на бок», и зелёным – «падение орлом вверх» (для фиксированного ζ толщина полоски определенного цвета равна вероятности).
По графику видно, что для какого-то ζ вероятности трёх событий будут равны. Уравнение можно точно решить, получив ζ = 1/√3 ≈ 0.577. Этот результат сильно отличается от вывода из известного геометрического решения: ζ = 1/2√2 ≈ 0.354. Идея геометрического решения в том, чтобы у всех трёх сторон был одинаковый телесный угол. Авторы статьи провели эксперимент, который показывает, что «динамическое» решение дает более правильный результат, чем «геометрическое».
Результаты
В ходе подготовки доклада на реферативный семинар у меня получилось разобраться в физике броска, явно выразить вероятности через начальные условия и ответить на поставленные вопросы:
- Для монеты номиналом один рубль вероятность упасть на ребро будет порядка 5%, однако в реальности вероятность может получиться другой, потому что в нашей модели монета падает на неупругую поверхность.
- Ширина монеты должна относиться к диаметру, как 1/√3 ≈ 0.577.
- Секрет броска заключается в правильном закручивании монетки вокруг вертикальной оси. Если угол ψ будет немного больше π/4, то визуально бросок не будет отличаться от «честного», но вероятность выпадения верхней стороны при будет близка к 100%.
Я считаю, что посещение реферативных семинаров действительно полезно. На них мы не просто разбираем интересные физические сюжеты и осваиваем новые приёмы решения задач. Мы готовимся к научной работе: учимся искать материал по теме, вникать в статьи и обсуждать их с коллегами.